In addition to the lecture notes, I took information from Jeff Bradberry's Intro to Monte Carlo Tree Searchas well as the original AlphaGo paper.

Formulating games as a minimax tree

Perfect information games are games where players have no information hidden from each other and no randomness, e.g. Go, chess, tic tac toe.

he maximin value is the highest value that the player can be sure to get without knowing the actions of the other players; equivalently, it is the lowest value the other players can force the player to receive when they know the player's action. Its formal definition is

In such a setting, we can compute the maximin value, i.e. the highest value that the player can be sure to get without knowing the actions of the other players. It is obtained by making each player play perfectly:

Where:

• $v_i$ is the value function of player $i$
• $a_i$ are the actions taken by player $i$
• $a_{-i}$ are the actions taken by all other players

Taking a turn-based game like chess for example, we can construct a game as a tree that contains all possible actions. At each level, the player chooses the action that maximizes her value. A winning strategy can be found by searching the game tree.

Because of the high branching factors of Go or chess (i.e. number of actions per turn), a full search is intractable.

Monte Carlo Tree Search

Monte Carlo Tree Search (MCTS) and its variant, Upper Confidence bound applied to Trees (UCT) don't require any domain knowledge. MCTS was one of the main ideas behind the success of AlphaGo (Deepmind).

In MCTS, any given board position can be considered a multi-armed bandit problem, if statistics are available for all of the child actions.

Borrowing from Jeff Bradberry's blog post, let's take the following tree, representing a game of Go for example, we're playing whites. $4/7$ means that taking this action resulted in $4$ wins over $7$ trials ($N$).

The first step is selection. We are selecting paths to evaluate. Selecting actions at random makes it unlikely that we'll find the one or two moves that are actually good, so we are selecting actions using an upper confidence bound algorithm, see the appendix for details. We iteratively apply UCB1 to select actions (nodes) until we reach a node that we haven't tried ($N=0$). This allows us to focus on high value regions of the search space.

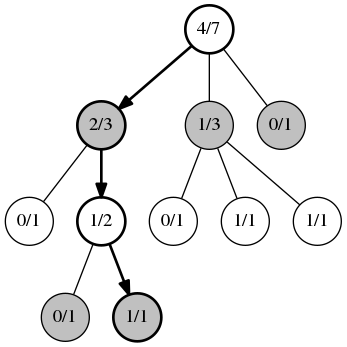
Now that we can no longer apply UCB1 (because we have no statistics and can't compute a mean reward or confidence interval), we select a new action at random. This second phase is the expansion.

The next step is simulation: we simulate the game, turn by turn, until terminal step using a random policy or simple heuristics. At the end of this simulation, the leaf node receives a reward.

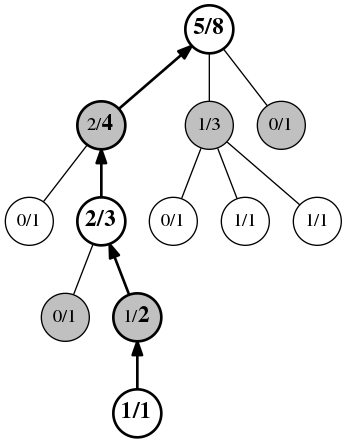
Finally, the fourth and last phase is the update, where we back-propagate the reward to all the positions visited during the playout. In the tree below, we suppose that whites won the playout, so we increment statistics: all the nodes in the path get a new visit $N := +1$, and all the white nodes get a new reward $R := +1$.

The tree structure of MCTS makes it massively parallelizable: each simulation rollout is independent of others.

Moreover, it only explores the part of the state space that is relevant from the current state by solving the Markov decision process from the current state onward and not solving for every state in advance. In comparison, dynamic programming methods such as value iteration or policy iteration require evaluating the entire state space (by backward induction over all states).

The simulation part of MCTS requires a model of the environment, whereas Q-learning is model-free: it learns Q-values directly through interaction with the environment.

MCTS can handle large or even infinite state spaces reasonably well because it only builds out the tree in regions it explores.

Appendix: upper confidence bound

In a multi-armed bandit problem, UCB1 is a classical exploration method. It tells you to pick the arm with highest upper confidence bound: $\mu_i +\sqrt{\frac{2 \ln n}{n_i}}$

This strategy has logarithmic regret $\mathcal{O}(\ln n)$. The $+$ becomes a $-$ when considering the actions of the opponent.

Applying MCTS to Go: deep dive into AlphaGo

Paper: Mastering the Game of Go with Deep Neural Networks and Tree Search