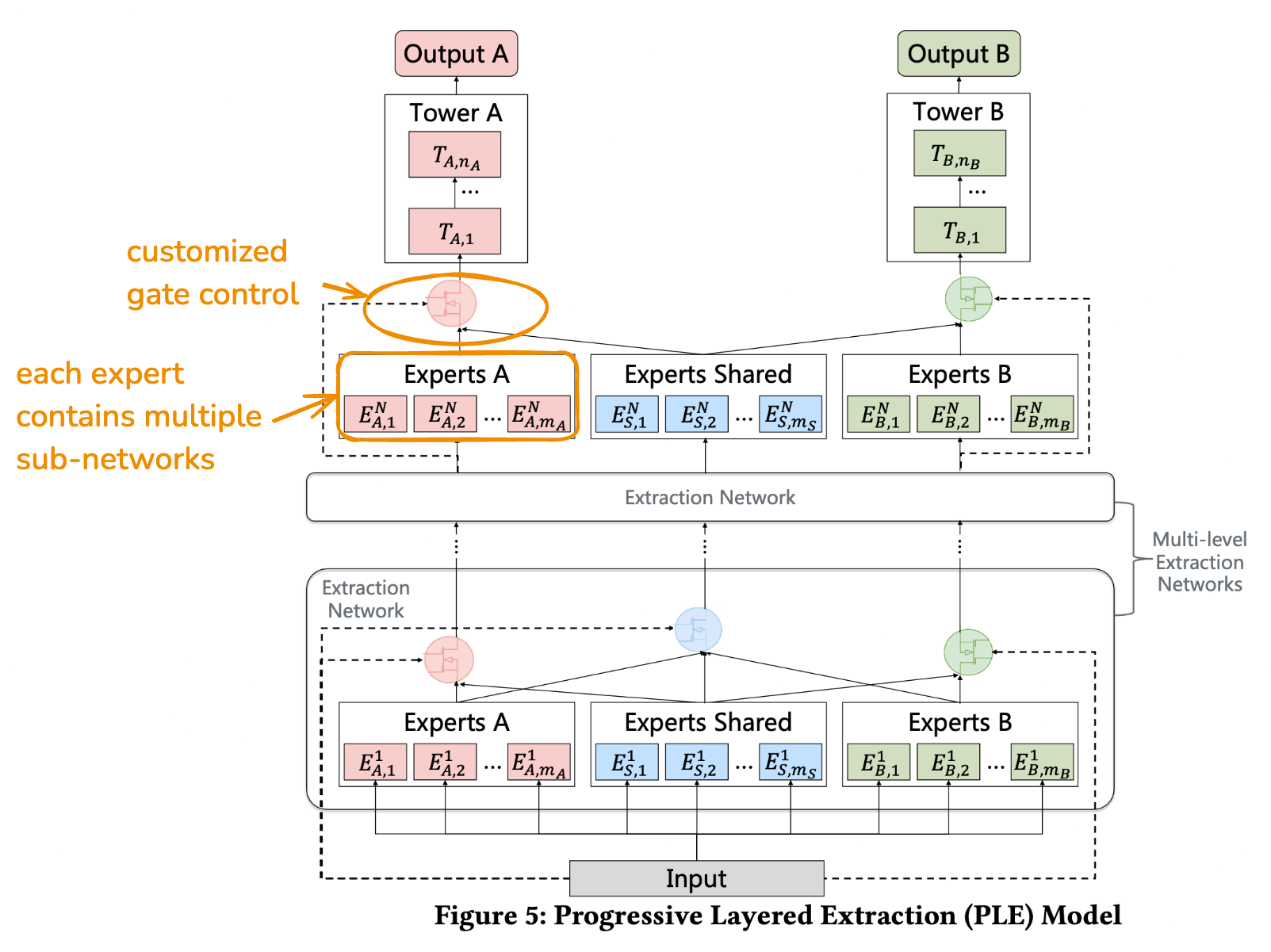
(PLE, by Tencent - 2020)

tldr

PLE separates task-common and task-specific experts to avoid parameter conflicts resulting from complex task correlations

• for each expert, a customized gate control fuses signals from the task specific experts and shared experts, based on a softmax + linear transformation of the expert's input (to handle sample dependent correlations between tasks).
• multiple such "extraction network" progressively separate task-specific and task-common representations

intro

Some challenges in multi-task learning

• negative transfer: the multi-task model performs worse than the single task model on some of the tasks, due to complex and competing task correlation in real-world recommender systems (especially sample dependent correlation patterns)
• seesaw phenomenon: performance on one task is improved by hurting the performance on some other tasks. Common MTL architectures struggle with improving performance across all tasks.

Tasks for the Tencent news feed video recommendation system:

• view completion ratio = $\frac{\text{number of complete views}}{\text{number of views}}$ (regression task trained with MSE loss)
• view through rate = $\frac{\text{number of complete views}}{\text{impressions}}$ (binary classification task trained with cross-entropy loss). A valid view is defined as a view that exceeds a certain threshold of watch time.
• share rate
• comment rate

The combination function they use is $p_{vtr}^{w_{vtr}}\times \dots \times p_{vcr}^{w_{vcr}}\times f(\text{video length})$, where $f$ is a non-linear transform function such as sigmoid or log. The weights are optimized through online experimental search to maximize online metrics.

Question: why use the weight as exponent?

Misc:

• They don't provide much details regarding the specific number of parameters used. For a valid comparison across models, it would seem fair to use the same FLOPs.
• They also report that AUC and MSE gains on view through rate and view completion ratio respectively, yields gains in online metrics.
• I like their "expert utilization" analysis, where they plot the mean and std of each expert's weight distribution, to show that the experts learned by the PLE are more differentiated than that learned by MMOE and multi-layer MMOE.

I'm trying to make a habit of paying attention to the dataset used. An average idea can show promise on easy datasets like MNIST.

Datasets used:

• proprietary dataset: user logs from the video recommender system serving Tencent News during 8 days. 46.9M users, 2.7M videos, 995M samples.
• census income dataset (public): contains 299,285 samples and 40 features extracted from the 1994 census database. Task 1 aims to predict whether the income exceeds 50k, task 2 aims to predict whether a person was never married.
• Ali-CPP dataset (public): 84M samples extracted from Taobao's recommender system (what is Taobao?). click through rate and conversion rate are two tasks modeling actions of click and purchase in the dataset.

architecture

main ideas:

• PLE separates task-common and task-specific experts to avoid parameter conflicts resulting from complex task correlations
• for each expert, a customized gate control fuses signals from the task specific experts and shared experts, based on a softmax + linear transformation of the expert's input (to handle sample dependent correlations between tasks).
• multiple such "extraction network" progressively separate task-specific and task-common representations

The network is composed of multiple "extraction network" layers. In the figure above, each extraction network is composed of:

• expert module A, which contains multiple sub-networks. It is responsible for extracting task specific patterns. It outputs a vector $\vec{E_A}$.
• expert module B, outputting: $\vec{E_B}$.
• shared expert module, responsible for learning shared patterns, outputting: $\vec{E_S}$

After each expert lies a customized gate control which fuses experts together, depending on the input or the lower-level fusion output. The reasoning is that the importance of each task varies a lot across inputs, and it is thus suboptimal to learn static weights for all samples (which results in the "seesaw" phenomenon). Let's look at the output of the gate control after expert $A$ at level $i$:

where $g^{(A, 0)}$ is set to the input $x$ and $W^{(A,i)}$ is a parameter matrix. The gating weights, generated by the softmax, thus only depend on the input.

For the gate control after the shared expert, we concatenate all experts: $[\vec{E_A}, \vec{E_B}, \vec{E_S}]$.

They jointly optimize all tasks in a weighed sum of losses. They mention the challenge of sequential user actions, causing the training space of different tasks to differ. For instance, a user can only share or comment after clicking on the item. Thus the set we would use for training "comment rate" is a subset of the set we would use to train "click rate". For rows that fall out of the training set on a specific task, they ignore the corresponding loss term.

comparison with MMOE

MMOE treats all experts equally and without differentiation, while PLE explicitly separates task-common and task-specific experts. While the MMOE theoretically contains this specification, it doesn't converge to it practice, as it requires setting some connections to zero.

Because the correlation patterns between view through rate (VTR) and view completion rate (VCR) is complex and "sample dependent", MMOE barely improves upon VCR mean squared error and VTR AUC.

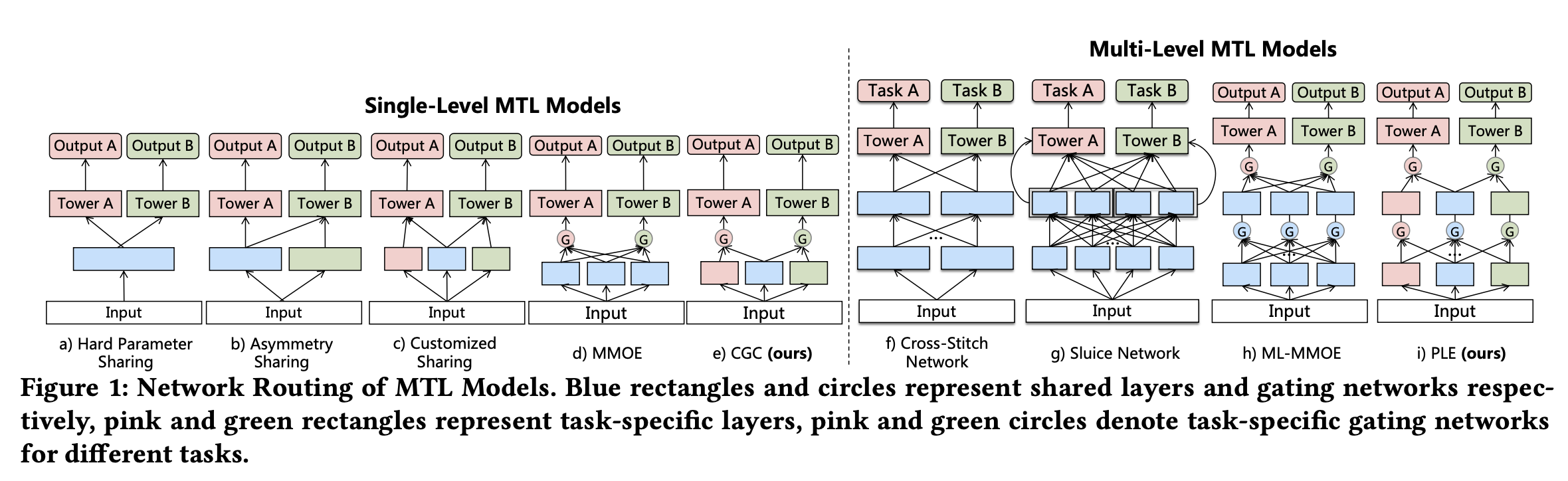
I like their concise overview of common multi-task models: