Batch normalization

Before the activation function, normalize each input dimension across the batch. If the input tensor $X\in \mathbb{R}^{(B, d)}$ where $B$ is the batch size:

where $i$ is the $i$-th dimension of input vector $X$ and the mean and standard deviation are computed across the vector $X_{[:, i]}$.

BatchNorm then applies some linear transformation (scale and shift): $Y_{[:,i]} = \gamma \hat X_{[:,i]} + \beta$ where $\gamma$ and $\beta$ are learned during training.

The main criticism is that normalization is dependent on batch samples which can lead to different behavior during inference (since batch statistics change).

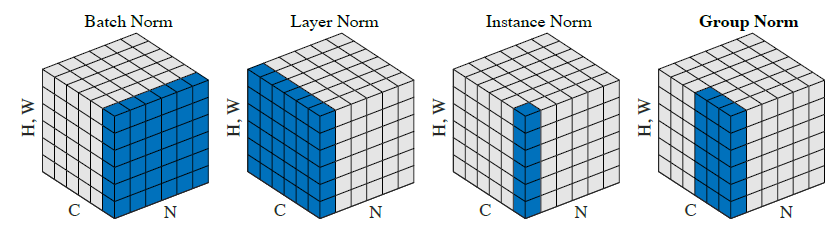
Batch norm is common for convoluted and fully connected networks.

LayerNorm

The key difference is that we normalize across the feature dimension (i.e. each sample in the batch is normalized individually): $X[i, :]$ instead of $X[:, i]$, which removes the training vs inference discrepancy.

LayerNorm is common in transformers, LSTMs and GRUs. It works well for small batch sizes (that would result in noisy estimates for batch norm, leading to unstable training). During inference, batch size can be 1 in LLMs and during training, the models are so large that batch size is small.

RMSNorm

Lighter alternative to layer norm that skips mean computation: $\text{RMSNorm}(X[i, :]) = \gamma\times\frac{X[i, :]}{\sqrt{\hat\sigma^2_d +\epsilon}}$ (bias $\beta$ is also omitted).

It is faster, utilizes less memory and achieves the same performance as LayerNorm. It was used in DeepSeekV3.

GroupNorm

This seems specific to convolutional networks. We normalize within groups of channels instead of across the batch or entire feature dimension.

Let's divide the channels (= features) across $G$ groups. For the first group, we normalize across:

where $i$ is the $i$-th sample in the batch and $d//G$ is the group size.

When the number of groups is $1$ ($G=1$), this is exactly layer norm.

When the number of groups is $d$ ($G = d$, the number of channels), this is exactly instance norm.

The specificity to images here is that we are actually considering only one pixel but we actually normalize across all $\text{height}\times\text{width}$ pixels together.

If $X\in\mathbb{R}^{(H\times W, B, d)}$ (2D image flattened into 1D vector), we normalize across: $X[:, i, 0:d//G]$.

The normalization parameter during the mean or standard deviation calculation is given by $\frac{1}{H\times W \times \underbrace{d//G}_{n_\text{groups}}}$

For instance norm, normalization happens per channel, per sample removing the dependency on other samples. It is especially used in style transfer and GANs.