Types

Four types of drift:

• concept drift: change in $P(y\vert x)$, shift in relationship between input and target output. If we have real-time ground truth labels, change in performance is the strongest indicator
• prediction drift: change in $P(\hat{y}\vert x)$
• label drift: change in $P(y)$, shift in ground truth distribution
• feature drift: change in $P(X)$

"Virtual concept drift" has no influence on performance:

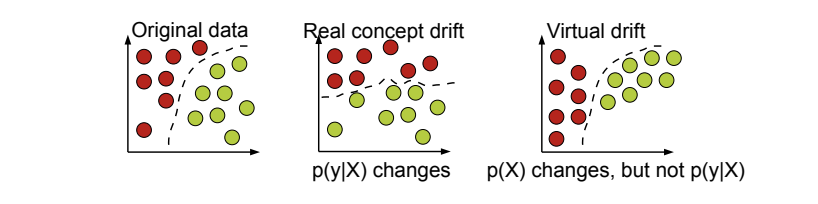
Causes

• externalities cause real change in data distribution
• data integrity issues due to data engineering or data collection

How to detect data drift?

No ground truth during inference, therefore cannot use performance metrics like AUC, precision, recall, etc...

Population Stability Index (PSI)

Mostly used in the financial industry

One training population and one scoring population. Divide each in say $n$ equal buckets, denoted $\{B_1^\mathcal{D}, \dots, B_n^\mathcal{D}\}$ where $\mathcal{D}$ is either the training or scoring dataset. For bucket $i$, let's denote $P_i^t$ the percentage of training data in bucket $B_i^\text{training}$ and $P_i^s$ the percentage of training data in bucket $B_i^\text{scoring}$.

$\text{PSI} = \sum_{1 \leq i \leq n} (P_i^s - P_i^t)\cdot \ln \frac{P_i^s}{P_i^t}$

• PSI < 0.1: no significant population change
• 0.1 < PSI < 0.2: slight population change
• PSI >= 0.2: significant population change

Kullback-Leibler divergence

Average number of bits wasted by encodings events from $P$ based on $Q$.

$D_{KL}(P\Vert Q) = \sum_{x\in \chi} P(x) \log \frac{P(x)}{Q(x)}$

Standard values?

Jensen-Shannon divergence

Based on KL divergence, except it is symmetric and always has a finite value

$JSD(P \Vert Q) = \frac{1}{2}D_{KL}(P\Vert M) + \frac{1}{2}D_{KL}(Q\Vert M), M=\frac{1}{2}(P+Q)$

Kolmogorov-Smirnov test

Nonparametric test (does not assume a specific distribution)

Largest absolute difference between two distributions functions:

$D = \sup_x \lvert F_\text{training}(x) - F_\text{scoring}(x)\rvert$

where the empirical distribution function for $n$ i.i.d. samples is given by: $F = \sum_{x} \mathbb{I}_{X_i \in (\infty, x]}$

If the scoring distribution comes from the reference distribution: $D \to 0$ almost surely as $n\to \infty$

Recall: sequence $X_n$ converges almost surely towards $X$ if $P(\lim_{n\to \infty} X_n = X) = 1$

Frameworks

scikit-multiflow for streaming data.

Papers to read

• https://arxiv.org/pdf/1010.4784.pdf
• https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.144.2279&rep=rep1&type=pdf
• https://link.springer.com/chapter/10.1007/978-3-540-28645-5_29