Source

Calibration refers to improving our model such that predicted probability distribution is similar to the probability observed in training data.

Calibration plot (=q-q plot)

Assume we are predicting probabilities for 2 classes $\{-1, 1\}$.

To produce a calibration plot

• sort by predicted probability $\hat p_i = \hat P(y=1 \vert X_i)$
• Define bins $B_i$ between $0$ and $1$ and compute $\hat p(B_i) = \frac{\sum_{k, \hat p_k \in B_i} \mathbb{I}_{y_k =1}}{\lvert B_i \rvert}$
• plot $\hat p(B_i)$ against expected true probability for the bin $p(B_i)$.

How do we derive $p(B_i)$? Think of it as first sampling a probability $p\sim\mathcal{U}[0,1]$, then, if $p\in[l, r]$ sample a random variable: $X\sim Bernoulli(p)$ taking value in $\{0, 1\}$.

What is the fraction of positives (i.e. the expectation of $X$) as $p$ varies between $l$ and $r$?

Perfect calibration plot should be identity:

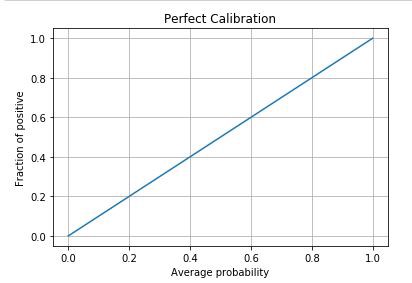
Pseudo-code:

import math

import seaborn as sns

def plot_calibration_curve_binary(label, y_proba):

	# expected true proba within a bin.

	def expected_proba(l, r):

		return 2/3 * (r**3 - l**3) / (r**2 - l**2)

	

	df = pd.DataFrame({

		"label": label,

		"y_proba": y_proba,

	})

	

	# rule of thumb for number of bars N given number of data points n: N = ceil(log2(n) + 1)

	N = math.ceil(math.log2(len(df) + 1))

	bins = pd.cut(df["y_proba"], bins=np.linspace(0, 1, N))

	

	calibration_df = df.groupby(bins, observed=False).agg(mean=("label", "mean"), count=("label", "count"))

	calibration_df["expected_proba"] = list(map(lambda x: expected_proba(x.left, x.right), calibration_df.index))

	

	sns.scatterplot(x=calibration_df["expected_proba"], y=calibration_df["mean"], label="y_proba")

	sns.lineplot(x=[0, 1], y=[0, 1], color="red") # perfect calibration line

	sns.despine() # remove top and right spines

Sigmoid / Platt calibration

Logistic regression on our model output:

Optimized over $\alpha$ and $\beta$.

Isotonic regression

Let $(\hat p_1, p_1), \dots, (\hat p_n, p_n)$. Isotonic regressions seeks weighted least-squares fit $\hat{p_i}^\text{new} \approx p_i$ s.t. $\hat{p_i}^\text{new} \leq \hat{p_j}^\text{new}$ whenever $\hat{p_i} \leq \hat p_j$.

Objective is: $\min \sum_{i=1}^n w_i (\hat p_i^\text{new} - p_i)^2 \text{ s.t. } \hat p_1^\text{new} \leq \dots \leq \hat p_j^\text{new}$ assuming the $p_i$'s are ordered.

This yields a piecewise constant non-decreasing function. To solve this we use the pool adjacent violators algorithm. See these notes.