Jan 2022

What are Automated market makers (AMMs)

• On a centralized exchange, the price of an asset is determined by a limit order book(matching highest bid with lowest ask).
• In a decentralized exchange (DEX) such as Uniswap, liquidity providers (LPs) provide a pair of tokens to a pool (e.g. ETH/BTC)

Invariants

• pool contains multiple coins (USDT, BTC, DAI, etc...) and price is determined by keeping a function of the coin supply to a constant: $f(x_1, x_2, \dots, x_n) = cst$.

• The price of the pair coin $i$ / coin $j$ is then $\frac{dx_i}{dx_j}$

• simplest case is two coins

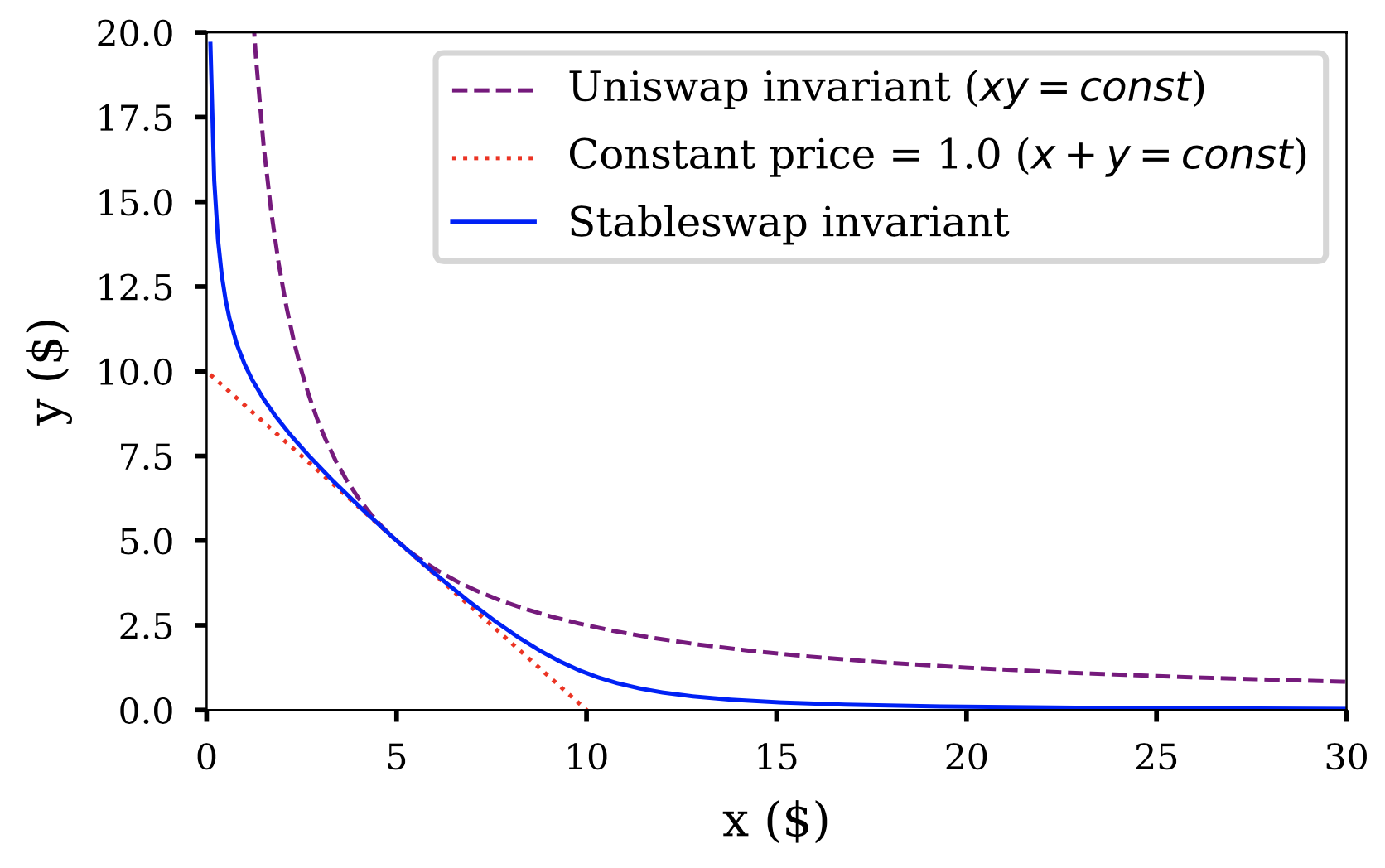
• Linear invariant: $x + y = k$ but the pool can be drained completely.

• constant product formula proposed by Vitalik and later popularized by Uniswap: $\underbrace{x}_{\text{balance of coin A}} \times \underbrace{y}_{\text{balance of coin B}} = k$ where $k$ is a constant balance of assets

• the only way to keep $k$ constant as orders come through is that $x$ and $y$ move in inverse directions. They don't move linearly however:

  

• this model can always provide liquidity by asymptotically raising the price of the coin as the desired quantity increases

• The price is given by the derivative (slope of the graph). In the Uniswap invariant model, the depth of the pool determines the slippage (see next sections)

• The Stableswap invariant combines both linear and Uniswap invariants (see paper):

  • the pool can slide up or down the linear invariant (price is constant) as long as the pools are somewhat balanced

  • when the pools fall out of balance, we switch to the uniswap invariant (swapping becomes expensive)

• Stableswap invariant for multiple coins: $\chi D^{n-1} \sum_i x_i + \prod x_i = \chi D^n + (D/n)^n$

• $\chi$ represents the amplification parameter of the linear invariant (magnifies the low slippage portion of the curve). We multiply by $D^{n-1}$ to make $\chi$ dimensionless.

• $D$ is the total amount of each coin, were they equal

• $\chi$ is dynamic: $\chi = A \frac{\prod x_i}{(D/n)^n}$. The ratio diminishes as the coins fall out of balance (the max of $\prod x_i$ is attained when all the $x_i = D/n$)

Uniswap invariant: price impact

• price is given by $p_A(B)=\frac{dy}{dx} = \frac{d\frac{k}{x}}{dx} = -\frac{k}{x^2}$

• imagine one wants to buy $\Delta y$ coins B. The price one will pay is $\Delta x$ and must respect:

  $\begin{aligned} (x + \Delta x) \times (y - \Delta y) & = x\times y \\ & = k \\ \Rightarrow \Delta x & = x(1/r_y - 1) \text{ where } r_y = \frac{y- \Delta y}{y} \in [0, 1] \text{ is the percentage of change in the supply of coin B} \\ \Leftrightarrow \underbrace{\frac{\Delta x}{\Delta y}}_{\text{price per unit of coin B}} & = \frac{x}{\Delta y}(\frac{y}{y-\Delta y} - 1) \\ & = \frac{x}{y} \frac{y}{\Delta y}\frac{\Delta y}{y - \Delta y} \\ & = \frac{x}{y}\frac{y}{y - \Delta y} \\ & = \text{base price}\times\frac{\text{size of supply before trade}}{\text{size of supply after trade}} \geq \text{base price} \end{aligned}$

  Therefore, if the pool increases, our order $\Delta y$ has less of an impact on the supply of coin B:

  $\begin{aligned} \frac{\partial \Delta x}{\partial x} & = 1/r_y - 1 = \frac{\Delta y}{y - \Delta y} = \text{size of order relative to new pool}\\ \frac{\partial \Delta x}{\partial y} & = -\frac{\Delta y}{(y - \Delta y)^2} \end{aligned}$

  We can see that:

    - as the supply of coin A increases, the rate of change of the price we will pay is smaller if the pool of coin B was larger to begin with
  
    - as the supply of coin B increases, the price we pay diminishes.
  

$x/y$ represents the price of the trading pair.

• front-running: if the miner places your order (therefore increases its price) and sells it to you at a higher price. You can set maximum slippage to avoid this.
• the premium makes it prohibitively expensive for whales to transact large size.
• price impact: after buying $\Delta y$ coins B for $\Delta x$ coins A, the token supply increases for A and decreases for B, therefore the next base price is $\frac{x - \Delta x}{y + \Delta y} \geq \frac{x}{y}$

Uniswap invariant: liquidity provider point of view

• Assume you add $\Delta x$ worth of coin A and $\Delta y$ worth of coin B. The new constant is $(x+\Delta x)\times(y + \Delta y)$ therefore the price of the pair coin A / coin B becomes $\frac{y + \Delta y}{x + \Delta x}$. If it is different than $\frac{y}{x}$, then an arbitrage opportunity arises between other exchanges. Thus we want: $\frac{y + \Delta y}{x + \Delta x} = \frac{y}{x} \Rightarrow \Delta x = \frac{y}{x}(r_x - 1), r_x = \frac{x+\Delta x}{x}$. That is, the token supply in the pool must increase at the same rate $\frac{\Delta y}{y} = \frac{\Delta x}{x}$
• liquidity providers get rewarded by charging a small exchange fee to the trader (0.3% for Uniswap)

Impermanent loss

• When the price of your tokens changes compared to when you deposited them in the pool.
• example: if the price of coin A increases on Binance compared to the pool, arbitrage traders buy the pair coin A / coin B (i.e. add coin B to the pool in exchange for coin A until the price of the pair reaches the target)
• the size of the pool increases so LPs might profit but they might have been better off hodling. The only thing impermanent loss cares about is the price ratio relative to the time of the deposit.
• source
• To read: https://research.paradigm.xyz/amm-price-impact

Let us denote:

• price of coin A in USD at time 0: $p_0^A$
• price of coin B in USD at time 0: $p_0^B$
• quantity of coin A in pool at time 0: $x_0$
• quantity of coin B in pool at time 0: $y_0$

Assume coin A experiences a return $r_A\in [-1, \infty)$, bringing it to price $p_1^A=(1+r_A)p_0^A$ at time 1.

Assume coin B experiences a return $r_A\in [-1, \infty)$, bringing it to price $p_1^B=(1+r_B)p_0^B$ at time 1.

Since there is no arbitrage opportunity at time 0, one must have $\frac{p_0^A}{p_0^B} = \frac{y_0}{x_0}$ (look at the dimensions of each variable to make sense of it)

Let us calculate quantities of coin A and B at time 1, $x_1$ and $y_1$, such that no arbitrage opportunity arises:

$p_1^A/p_1^B = x_1/y_1 \Rightarrow x_1 p_1^A/p_1^B = y_1$

Moreover, by the constant product formula: $x_1y_1 = k = x_0y_0$

Therefore:

$\begin{aligned}x_1^2 \frac{p_1^A}{p_1^B} & = x_0y_0 \\\Rightarrow x_1^2 \gamma \frac{p_0^A}{p_0^B} & = x_0y_0, \gamma = \frac{1+r_A}{1+r_B} \\\Rightarrow x_1^2 \gamma \frac{y_0}{x_0} & = x_0y_0 \\\Rightarrow x_1 = \frac{1}{\sqrt{\gamma}}{x_0} \text{ and } y_1 = \sqrt{\gamma} y_0\\\end{aligned}$

The return of holding the coins is:

$\begin{aligned}r_{hold} & = \frac{p_1^Ax_0 + p_1^By_0}{p_0^Ax_0 + p_0^By_0}\\\Rightarrow r_{hold} & = \frac{p_0^A(1+r_A)x_0 + p_0^B(1+r_B)y_0}{p_0^Ax_0 + p_0^By_0}\\\Rightarrow r_{hold} & = \frac{(1+r_A)+(1+r_B)}{2}\text{ since }p_0^A x = p_0^B y\text{ by the no-arbitrage argument above}\end{aligned}$

Similarly, the return of providing liquidity (assuming no LP fees):

$\begin{aligned}r_{pool} & = \frac{p_1^A x_1 + p_1^B y_1}{p_0^A x_0 + p_0^B y_0}\\r_{pool} & \underbrace{=}_{\text{ replacing quantities at time 1 by their formulas + no-arbitrage argument}} \frac{(1+r_A)\frac{1}{\sqrt{\gamma}} + (1+r_B)\sqrt{\gamma}}{2}\end{aligned}$

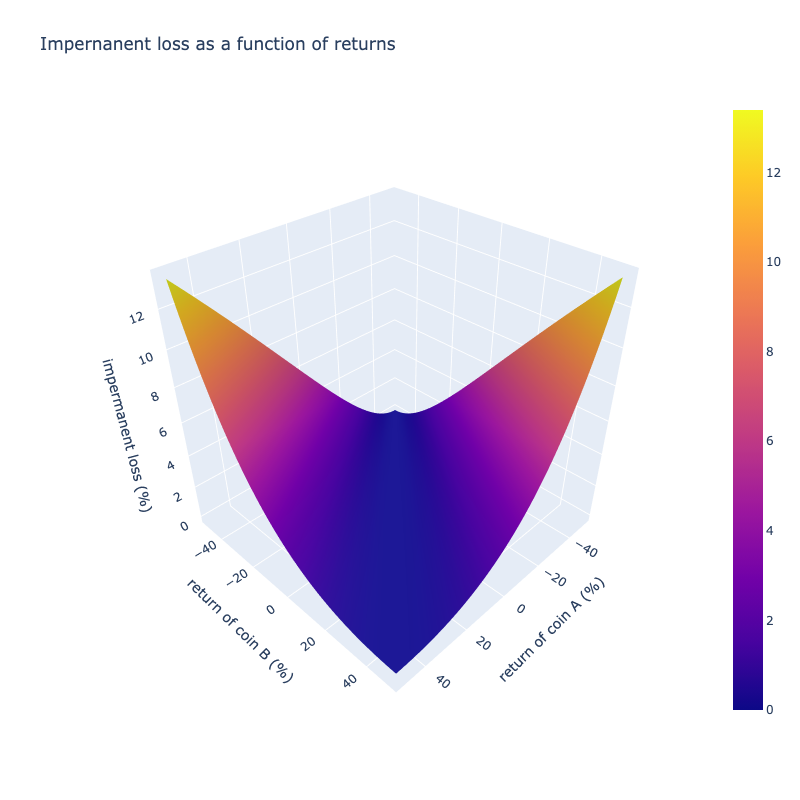
Finally, the impermanent loss can be computed as:

$\text{loss} = \frac{r_{hold}-r_{pool}}{r_{hold}} = 1 - \frac{r_{pool}}{r_{hold}} = 1 - \frac{(1+r_A)\frac{1}{\sqrt{\gamma}} + (1+r_B)\sqrt{\gamma}}{(1+r_A)+(1+r_B)}$

We can see this doesn't depend on the quantities or prices of the coins but merely their returns. The formula is also symmetrical in coin A or B, regardless of initial quantities and prices. Plotting the impermanent for different values of $r_A$ and $r_B$:

Curve

• Curve is a stablecoin DEX (exchange between similar ERC-20 tokens such as USDC/DAI an WBTC/renBTC in order to minimize impermanent loss)
• Assume you are a whale, sitting in stablecoin (e.g. USDC) and you need to trade for another stablecoing (e.g. MIM), you want to minimize slippage by minimizing fees (0.3% for Uniswap vs 0.04% for Curve) and maximizing ilquidity to remain as close as 1:1 as possible.
• Curve TVL (total value locked): $23bn / Uniswap (next leading DEX):$8bn
• Curve has a governance token named CRV. Users can lock their CRV in exchange for vote escrowed-CRV (i.e. veCRV) and a 50% share of each trading fee proportional to their locked amount.
• veCRV vote each week to which liquidity pools the set of CRV emissions will be directed (aka gauge weights)
• Projects don't need to incentivize liquidity holders with their native tokens if their pools get CRV tokens (i.e. a passive income). https://twitter.com/JackNiewold/status/1476334616797749248
• Projects want their pool (e.g. MIM3CRV) to suffer minimal slippage and de-pegging. They want their coin to be the most liquid stablecoin. They can buy up CRV, lock it in exchange for evCRV and sway the vote to ensure that emissions are going towards their pool. However, a more cost-effective way is to bribe veCRV holders individually / the largest holder of veCRV (i.e. Convex)

Convex

• Convex allows LPs to deposit CRV and receive the boosted CRV rewards as if they had locked their CRV for veCRV.

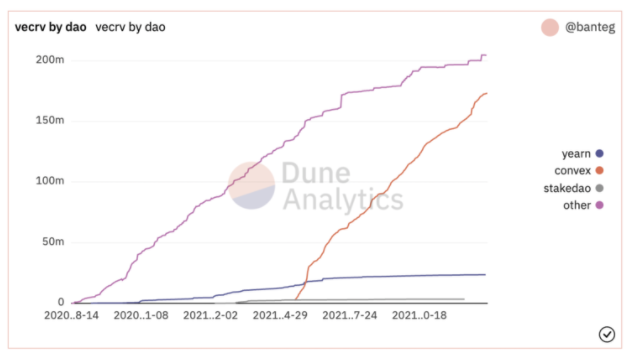
• They still use Curve on the back end, but they enable the boosted rewards through the amount of CRV that they amassed over the past 6-8 months:

  

• convert CRV to cvxCRV (liquid unlike veCRV), stake cvxCRV and earn CVX, trading fees (normal veCRV rewards: 50% of trading fees), airdrops and 10% of the platform's CRV earnings.

• when you lock CRV in return for cvxCRV, on the back end you are perpetually locking up your CRV (although you can trade cvxCRV for CRV)

• Andre Cronje created [[bribe.crv.finance]]. Protocols can put up a set amonut of their native token to encourage veCRV holders to vote in favour of their pool.

• Convex has their own voting platform now.